(In memoria di Pierluigi Friello)

Francesco Aucone, Graziella De Gasperi

Premessa

Come si comportano le strutture complesse, sia naturali che artificiali, quando vengono investite da onde elastiche di diversa natura ed energia?

Spesso, insieme all’amico e collega Pierluigi Friello, abbiamo avuto diverse occasioni per approfondire questo e altri aspetti della dinamica sperimentale e ne abbiamo approfittato ogni qualvolta la professione ci ha fornito la possibilità di farlo.

In particolare qui sono descritti due studi sperimentali riguardo alcuni aspetti del comportamento dinamico di due strutture complesse: un edificio di Roma e i terreni alluvionali di un tratto della Val Nerina. Apparentemente queste strutture non hanno niente in comune se non il fatto che ambedue sono state investite dall’energia dinamica di alcuni eventi della crisi sismica che ha interessato il centro Italia nell’estate-autunno del 2016.

L’Edificio

Nell’Ottobre del 2016, su richiesta di un laboratorio ufficiale dell’hinterland romano, eseguimmo diversi monitoraggi delle vibrazioni su un edificio situato in Piazza dei Navigatori a Roma.

Lo scopo del monitoraggio era quello di valutare se le vibrazioni, provocate dal traffico veicolare e registrate in vari punti dell’edificio, potessero creare dei problemi all’integrità strutturale dello stesso, ma specialmente valutare se le stesse potessero arrecare disturbo psico-fisico agli abitanti.

Oltre a tenere fede all’incarico conferitoci, decidemmo di sfruttare l’occasione per approfondire i nostri studi sul comportamento dinamico degli edifici.

Posizionammo così tre terne geofoniche su tre diversi piani dell’edificio di Piazza dei Navigatori e registrammo le vibrazioni ambientali per la durata di 24 ore. Avendo come scopo, oltre quello per cui eravamo stati incaricati, anche quello di studiare il comportamento dinamico della struttura, posizionammo i sensori allineati lungo una ideale colonna verticale e facemmo in modo che le misure fossero sincronizzate temporalmente mediante il collegamento dei tre sensori alla rete satellitare GPS. Facemmo in modo anche, ovviamente, che le direzioni assiali dei sensori fossero allineate.

Questa configurazione ci ha permesso, nella fasi di analisi, di processare i dati dinamici registrati con una tecnica appartenente alla teoria dei segnali conosciuta come “correlazione incrociata”¹.

Senza dilungarsi troppo sulla descrizione matematica di tale tecnica analitica, non essendo questo lo scopo dell’articolo, basti considerare che essa permette di estrarre le frequenze naturali di oscillazione di una struttura dal contenuto spettrale di una registrazione, effettuata sincronicamente su almeno due punti notevoli della stessa, senza conoscere a priori l’input. Con questa tecnica è infatti possibile ottenere le frequenze di risonanza della struttura senza il bisogno di eccitarla artificialmente, ma utilizzando come input dinamico il campo delle microvibrazioni ambientali.

Le funzioni matematiche principali di questa tipologia di analisi sono tre: il cross spettro, ottenuto dalla trasformata di Fourier (FFT) della funzione di cross correlazione, lo spettro di fase e la funzione di coerenza.

Il primo comprende il contenuto spettrale comune ai due punti di misura correlati, lo spettro di fase descrive la differenza di fase in gradi tra i due movimenti e la terza funzione ci dice se i due segnali , per una certa frequenza, siano coerenti o meno, e fisicamente può essere interpretata come la descrizione di quanto si conservi la differenza di fase nel tempo.

Le frequenze naturali di oscillazione di una struttura sono quelle per cui, nell’analisi incrociata, la differenza di fase tra i due movimenti è di 0° o 180° (o perlomeno molto vicina a tali valori), e il valore della coerenza è prossimo ad 1.

È importante sottolineare che la completezza dell’analisi dinamica di una struttura si raggiunge quando si determinano i modi di vibrare della stessa, di cui la frequenza è solo uno dei termini necessari a caratterizzarli. Un modo di vibrare è infatti rappresentato da tre grandezze: la frequenza naturale di oscillazione, la deformata e lo smorzamento strutturale.

Tuttavia per effettuare un’accurata analisi che ci restituisca una vera e propria “carta d’identità dinamica” di una struttura servono molte misure, il cui numero è funzione anche del numero di sensori che si hanno a disposizione. Ma già arrivare a conoscere le frequenze di risonanza della struttura può sicuramente fornirci informazioni importanti su quello che potrebbe essere il suo comportamento nel caso fosse investita dalle vibrazioni causate da un evento sismico di cui si conoscano livelli energetici e contenuto spettrale.

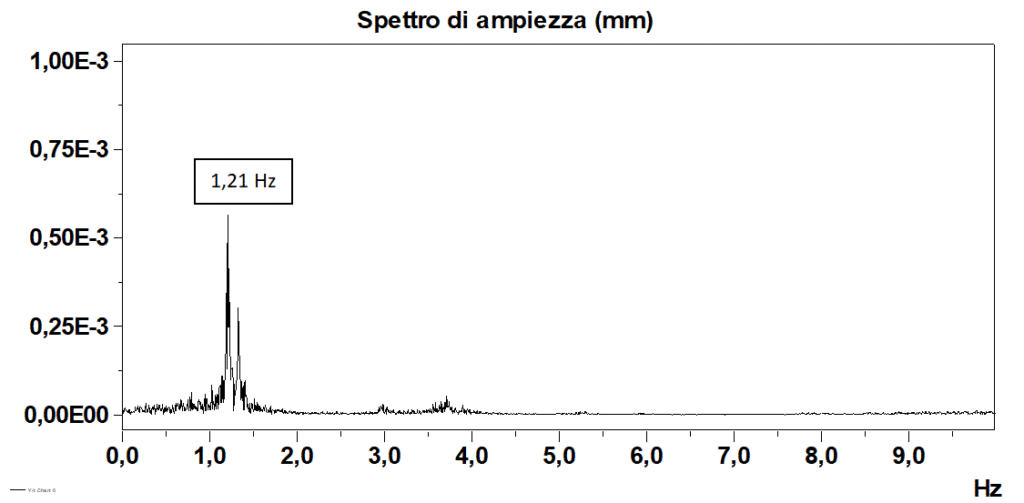
Ritornando al nostro edificio, l’analisi di cross correlazione, condotta utilizzando come input le microvibrazioni ambientali, ci ha permesso di ottenere la frequenza fondamentale naturale di oscillazione orizzontale lungo la direzione meno rigida “Y” della struttura (Figura 1). Nella Figura 2 sono osservabili le tre funzioni della cross correlazione con una frequenza di oscillazione naturale di 1,21 Hz, caratterizzata da una differenza di fase di 1° ed una coerenza di 0,99.

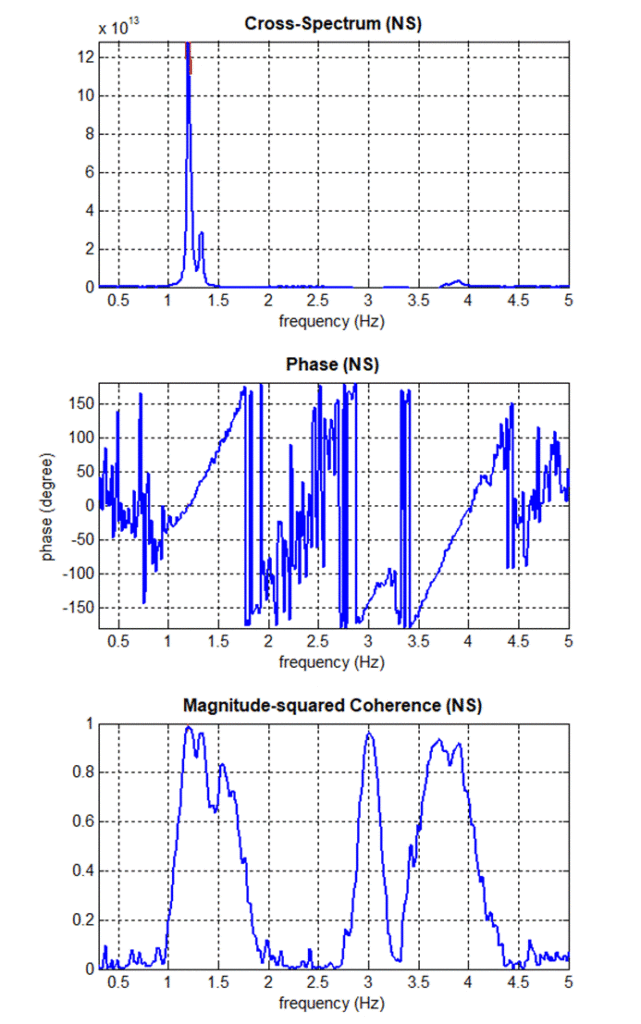
L’analisi poteva essere considerata conclusa con la determinazione della frequenza naturale di oscillazione orizzontale lungo “Y”, se non fosse che durante le 24 ore di monitoraggio i sensori posizionati nell’edificio, oltre alle vibrazioni ambientali, hanno registrato tre scosse di terremoto legate alla crisi sismica che ha investito l’Italia centrale durante il 2016-2017. Questa “fortunata” coincidenza ci ha permesso di approfondire ancora di più gli aspetti dinamici sperimentali legati al comportamento della struttura.

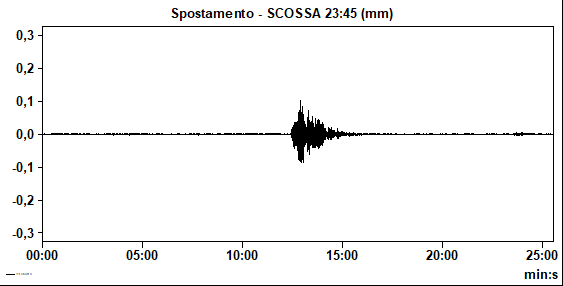
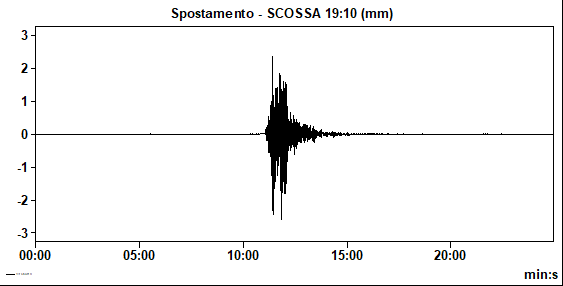
Di queste tre scosse una ha causato oscillazioni orizzontali dell’ordine dei 0,1 mm, mentre le altre due hanno fatto oscillare l’edificio orizzontalmente con spostamenti massimi dell’ordine dei 2,5 mm. Questo ha permesso di osservare il diverso comportamento della struttura dal punto di vista della sua risposta in frequenza.

Sono stati messi a confronto i vibrogrammi e gli spettri di Fourier di tre registrazioni effettuate nella medesima stazione del fabbricato, di cui la prima relativa ad un periodo con assenza di scosse sismiche, con oscillazioni orizzontali ambientali dell’ordine dei 5 micron, la seconda relativa alla scossa che ha causato un oscillazione massima di circa 0,1 mm, ed una terza relativa ad una scossa sismica che ha causato oscillazioni massime di circa 2,5 mm.

Il dato più importante che è emerso è che con l’aumento dell’energia sismica, ed il conseguente aumento dell’oscillazione, la frequenza naturale dell’edificio tende ad assumere valori più bassi, specialmente quando la deformazione supera certi valori, rivelando un comportamento dinamico non lineare anche in assenza di deformazioni permanenti della struttura.

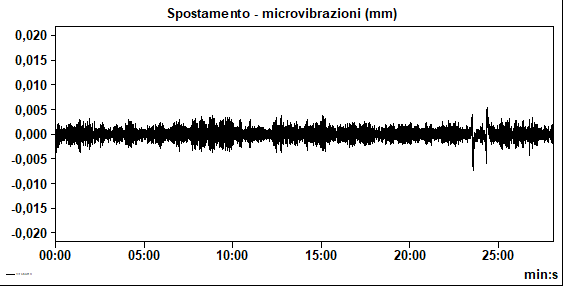
Nelle Figure 3a e 3b sono riportate, rispettivamente, la time history di una parte di microvibrazioni ambientali ed il relativo spettro di Fourier ottenuto con la FFT, con una frequenza di 1,21 Hz, che è quella classificata come frequenza naturale di oscillazione dell’edificio in direzione Y, grazie ai risultati dell’analisi di cross correlazione.

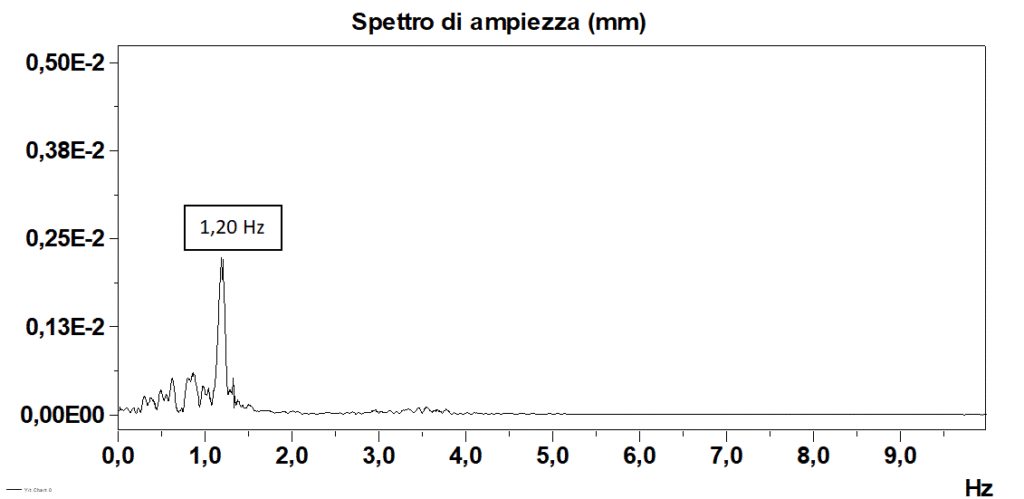
 Nelle Figure 4a e 4b sono riportate la time history di una scossa sismica relativamente a bassa energia (spostamento massimo di circa 0,1 mm) ed il relativo spettro di Fourier ottenuto con la FFT, con una frequenza di picco di 1,20 Hz.

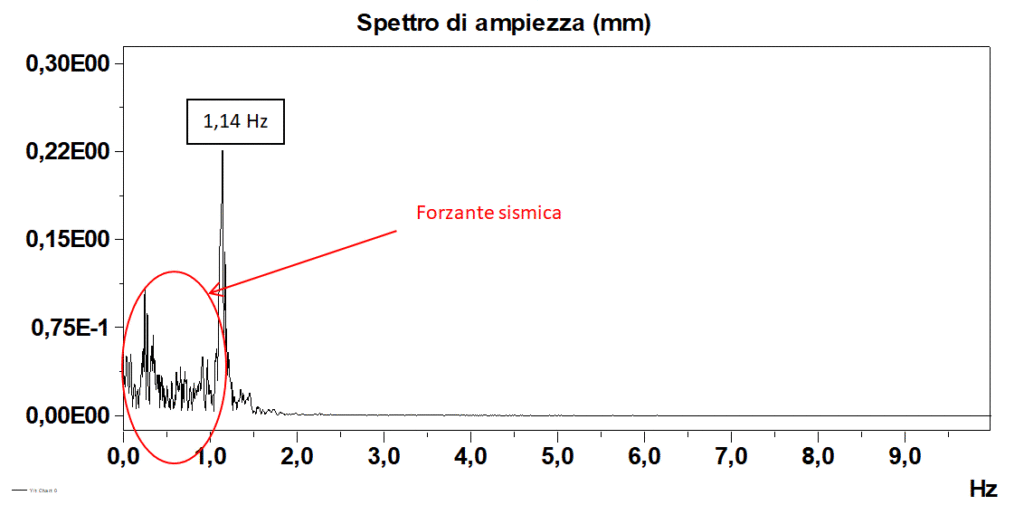
Nelle Figure 5a e 5b, infine, abbiamo rispettivamente la time history di una scossa sismica relativamente a più alta energia (spostamento massimo di circa 2,5 mm) ed il relativo spettro di Fourier ottenuto con la FFT, con una frequenza di picco di 1,14 Hz.

Negli spettri si nota inoltre che, man mano che aumenta l’energia sismica, le frequenze della forzante terremoto divengono sempre più importanti, energeticamente, nei confronti di quelle legate alla risposta dell’edificio.

Altro elemento di analisi che scaturisce dall’osservazione degli spettri è che il contenuto in frequenza della forzante sismica ha in questo caso valori abbastanza distanti rispetto alla frequenza naturale dell’edificio, per cui durante il breve periodo di imposizione della forzante non si sono verificati episodi di risonanza.

Il terreno

Negli anni 2018-2019, in occasione dell’espletamento dell’incarico relativo al “Progetto esecutivo per la messa in sicurezza del Centro Faunistico del Cervo e Recupero degli Animali Selvatici di Castelsantangelo sul Nera”, in territorio appartenente al Parco Nazionale dei Monti Sibillini, abbiamo effettuato diverse misure delle microvibrazioni ambientali. La Val Nerina e l’intero territorio del Parco erano stati da poco interessati dalla crisi sismica del 2016-2017, con numerosi e forti eventi dinamici che, oltre a provocare il crollo di numerosi edifici, ha innescato numerose frane modificandone geomorfologicamente  l’assetto in maniera molto profonda.

Oltre all’espletamento dell’incarico, le misure di sismica passiva effettuate in sito e la rielaborazione dei sismogrammi appartenenti ad alcuni dei più significativi eventi sismici che hanno colpito il territorio, ci hanno permesso di studiare il comportamento di una copertura dal punto di vista del rapporto spettrale tra componenti orizzontali e verticale del moto. È questo un aspetto che, riguardo alla gestione di un territorio altamente sismico, ha dei risvolti molto pratici inerenti il fenomeno della doppia risonanza tra copertura sedimentaria ed edificio ubicato sulla stessa.

Spesso, per esempio, sulle MOPS del 1° livello della MS sono indicate le frequenze di risonanza delle successioni sedimentarie, determinate mediante la tecnica di analisi delle microvibrazioni ambientali di Nakamura. E spesso si da una valenza tecnica a questi valori di frequenza, nel senso che una eventuale struttura esistente o di nuova costruzione è meglio che abbia i propri modi di vibrare con frequenze lontane da quelle delle coperture su cui si trovano o saranno costruite. Ma che succede durante un sisma al rapporto HV? Valgono ancora i presupposti della doppia risonanza determinati in regime di microvibrazioni ambientali?

Per rispondere a queste domande abbiamo dapprima individuato una stazione sismica ubicata sul territorio comunale di Castelsantangelo sul Nera, abbiamo effettuato delle misure delle microvibrazioni ambientali in adiacenza al punto della stazione ed infine abbiamo ricavato le curve HV degli eventi sismici e delle microvibrazioni e le abbiamo confrontate tra loro.

L’elemento più importante che è scaturito dal confronto è che durante l’applicazione di un’azione sismica generata da una sorgente sismogenica vicina, i rapporti spettrali relativi alle registrazioni del campo delle microvibrazioni ambientali, vengono completamente stravolti. Ma proseguiamo per gradi.

Stazione sismica

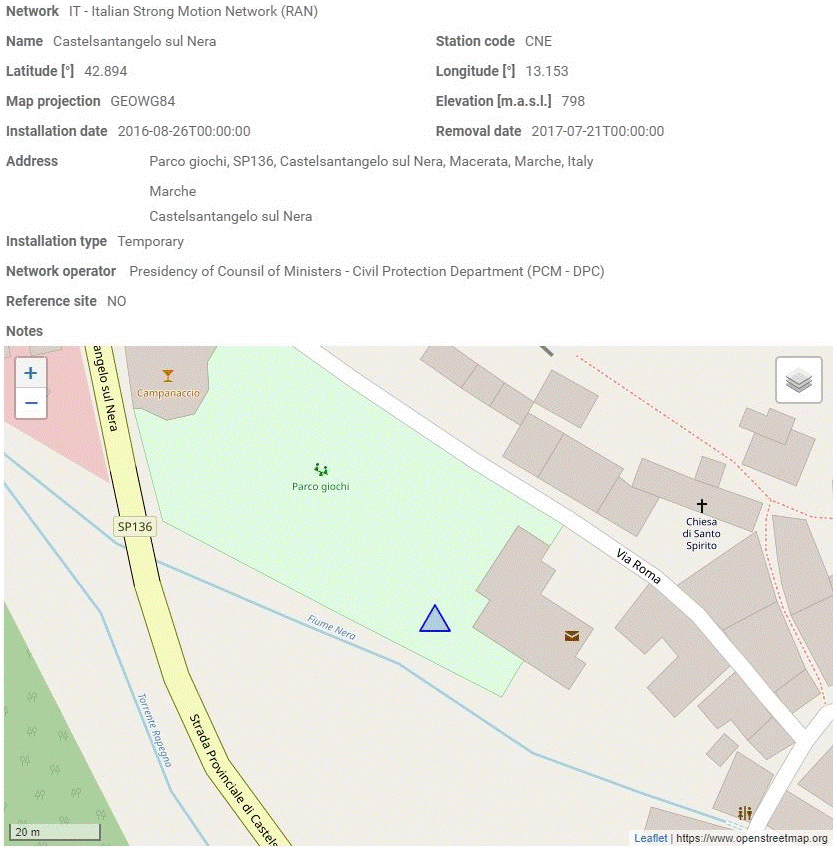
La stazione sismica individuata è quella dell’Italian Strong Motion Network (RAN) con codice CNE e denominata Castelsantangelo sul Nera (Figura 6), situata nel parco giochi in adiacenza al municipio, su un terreno con categoria sismica presunta C. Installata nel 26 Agosto 2016 e rimossa il 21 Luglio 2017. Dall’Engineering Strong Motion Database (https://esm-db.eu) ci siamo scaricati i sismogrammi di due eventi sismici registrati dalla stazione:

EMSC-20161026_0000077 del   2016-10-26, alle ore UTC 17:10:36, caratterizzato da una Mw = 5.4, distanza epicentrale 3.2 Km e profondità ipocentrale 8.1 Km.

EMSC-20161026_0000095 del   2016-10-26, alle UTC 19:18:06, caratterizzato da una Mw = 5.9, distanza epicentrale 2.5 Km e profondità ipocentrale 7.5 Km.

La stazione era situata a livello del suolo, al di sopra delle coperture alluvionali del Fiume Nera (Figura 7)

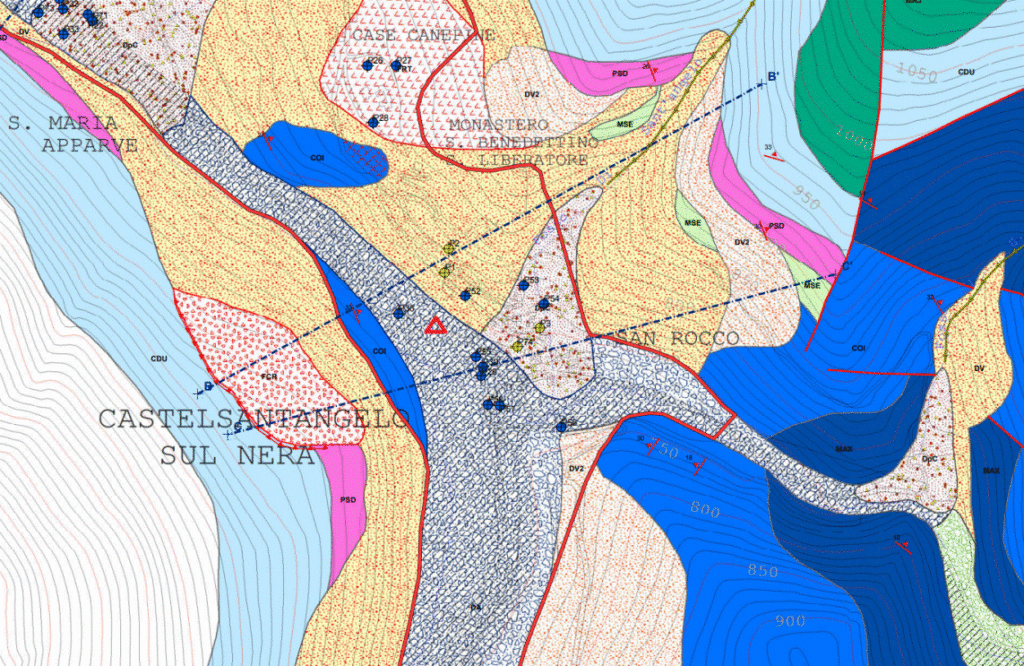
Misura delle microvibrazioni ambientali e confronti tra le HV ambientali e quelle relative a tre eventi sismici

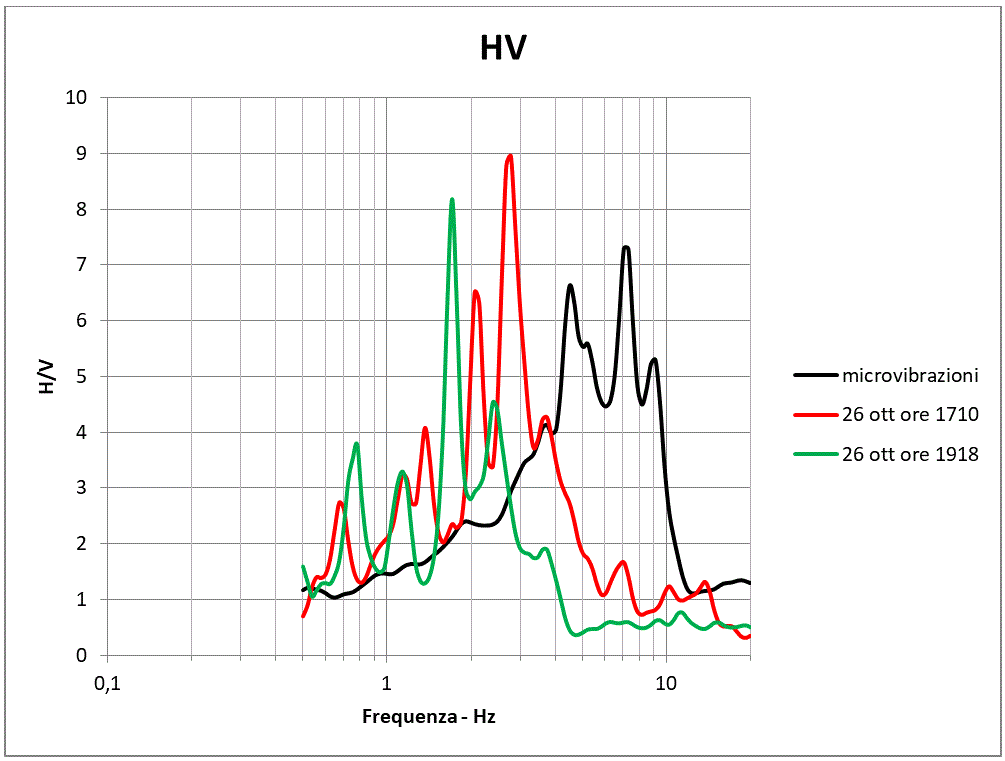
In figura 8 è riportato il risultato dell’elaborazione della misura delle microvibrazioni ambientali effettuate in adiacenza al punto di collocazione della stazione sismica (Foto 1 e 2).

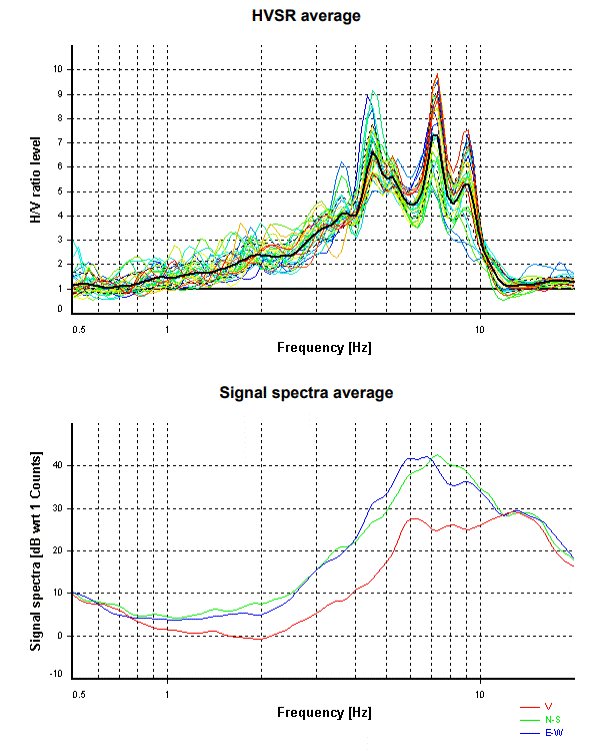
Nella curva HV si notano tre massimi (4.5 Hz, 7 Hz e 9 Hz) classificabili con ragionevole certezza, vista la forma delle singole componenti spettrali, come frequenze dovute alla presenza di altrettanti contrasti d’impedenza sismica.

Nelle prossime due figure (Figure 9 e 10) vengono riportati i risultati dell’analoga analisi condotta sui sismogrammi dei due eventi sismici prima elencati.

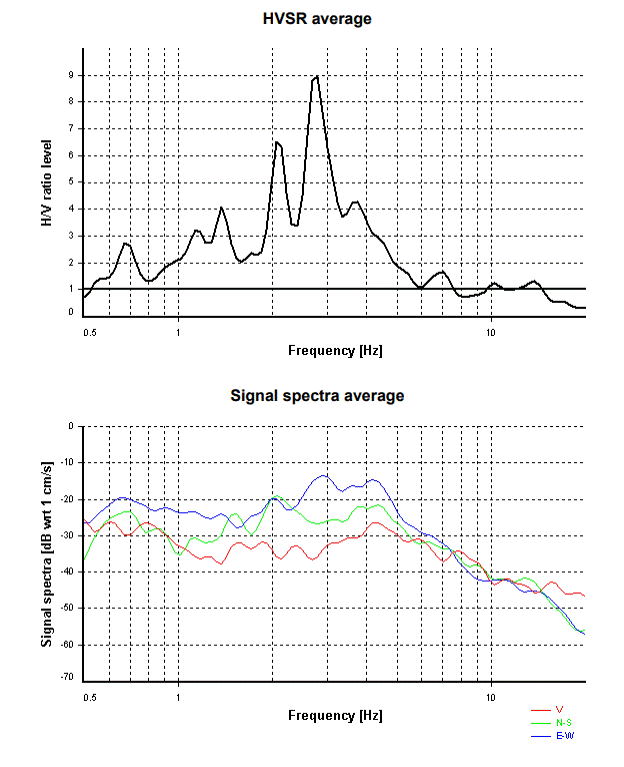
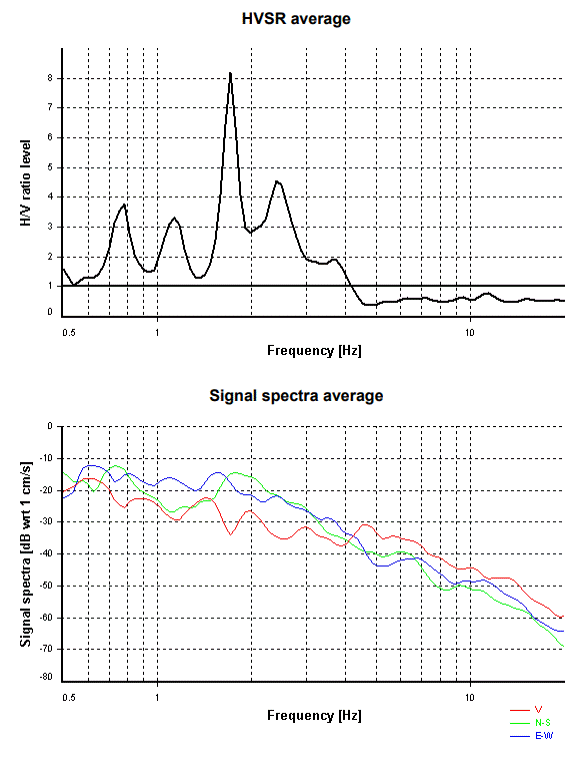
Infine nella Figura 11 viene riportato il confronto tra le curve HV delle microvibrazioni e quelle dei due eventi sismici.

Note:

1.” In teoria dei segnali la correlazione incrociata (detta anche correlazione mutua o cross-correlazione, dall’inglese cross-correlation) rappresenta la misura di similitudine di due segnali come funzione di uno spostamento o traslazione temporale applicata ad uno di essi.” – da: https://it.wikipedia.org/.